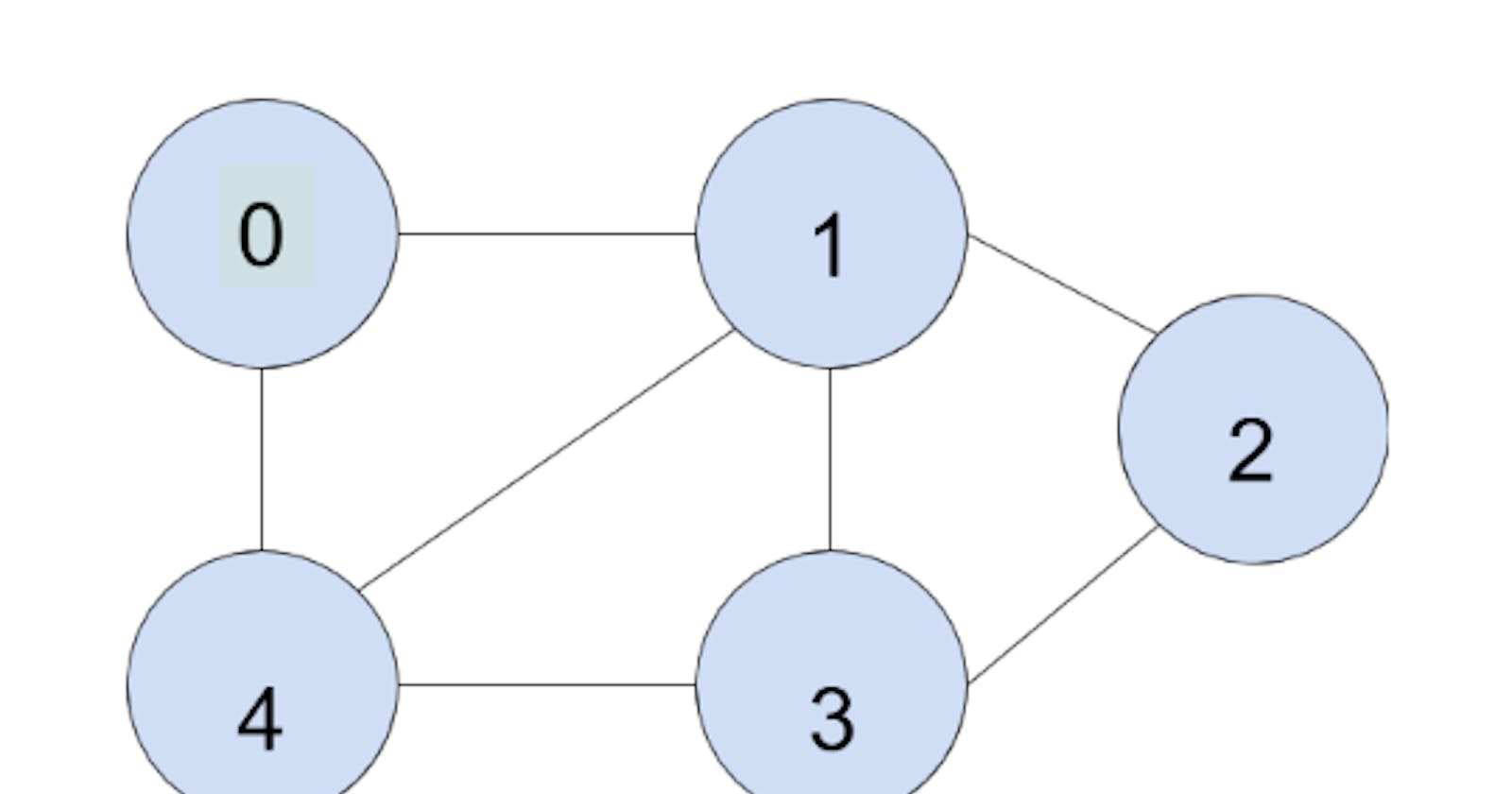
Graph Representation: Adjacency List vs Adjacency Matrix

A Graph is a non-linear data structure consisting of vertices and edges. It's one of the most important data structure with many real-life applications like in social networks, routing, telephone network, and circuit network

It consists of two components :

A finite set of vertices or nodes.
A set of finite ordered pairs of the form (u, v) are known as the edge.

Graph Representation

Let G = (V, E) where V is the set of vertices and E is the set of edges, where each edge is represented as a tuple of vertices.

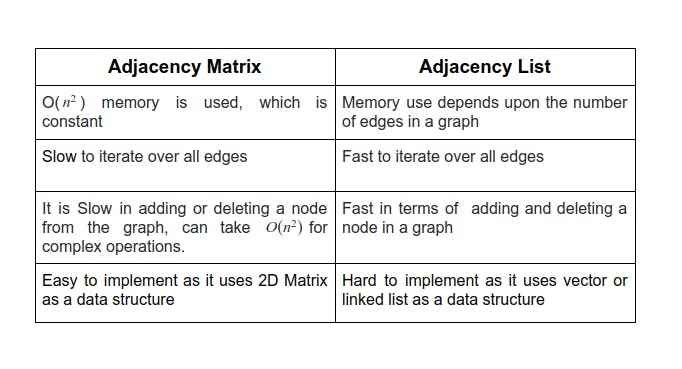
There are two most commonly used representations of a graph.

Adjacency Matrix
Adjacency List

Graphs can also representations with Incidence Matrix and Incidence List. The choice of the graph representation depends on the type of operations performed and the algorithm to be used.

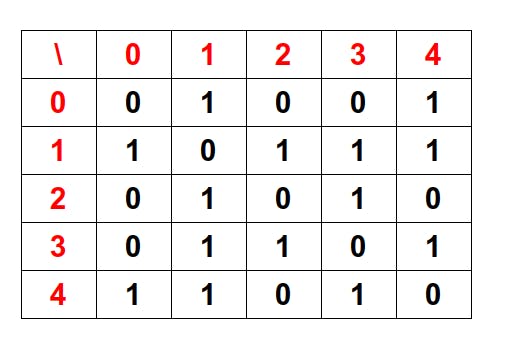
Adjacency Matrix

Adjacency Matrix is a |V| × |V| two-dimensional array where V is the vertices of a graph. Element (i, j) in a matrix is 1 if and only if an edge E (vi,vj) is present.Thus, an adjacency matrix takes up Θ(|V|²) storage. The adjacency matrix for the undirected graph is always symmetric. For weighted graph adj[i][j] will be equal to w this means that there is an edge from vertex i to vertex j with weight w.

Algorithm for adjacency matrix

Create a matrix A of size NxN Initialise it with zero Now, Iterate over each edge given in form (u,v)
Assign 1 to A[u][v] : If graph is undirected then assign 1 to A[v][u].

Implementation of the adjacency matrix

class Graph:
    """
    Adjacency Matrix Representation in Python
    """

    # Initialize the matrix
    def __init__(self, size):
        self.adjMatrix = [[0 for _ in range(size)] for _ in range(size)]
        self.size = size

    # adding edge from vertex v1 to v2
    def addEdge(self, v1, v2):
        self.adjMatrix[v1][v2] = 1
        self.adjMatrix[v2][v1] = 1

    # deleting edge
    def delEdge(self, v1, v2):
        self.adjMatrix[v1][v2] = 0
        self.adjMatrix[v2][v1] = 0

    # length of graph
    def __len__(self):
        return self.size

    # printing matrix
    def printMatrix(self):
        for row in self.adjMatrix:
            print(*row)
            print


def main():
    graph = Graph(5)  # init graph of size 5
    graph.addEdge(0, 1)
    graph.addEdge(0, 2)
    graph.addEdge(1, 2)
    graph.addEdge(2, 0)
    graph.addEdge(2, 3)

    graph.printMatrix()


if __name__ == "__main__":
    main()

Output : 0 1 1 0 0 1 0 1 0 0 1 1 0 1 0 0 0 1 0 0 0 0 0 0 0

Pros:

Easy to implement and understand.
Removing any edge takes O(1) time.
Queries such as finding edge from vertex ‘u’ to vertex ‘v’ are efficient and can be done O(1).

Cons:

Consumes more space O(V²).
Even for a sparse graph, it takes same space and adding a vertex is O(V²) time.

Adjacency List

An adjacency list is a list of lists and each list is connecting to a vertex u, which contains a list of edges that originate from u. So, an adjacency list takes Θ(V + E) space in the worse case.

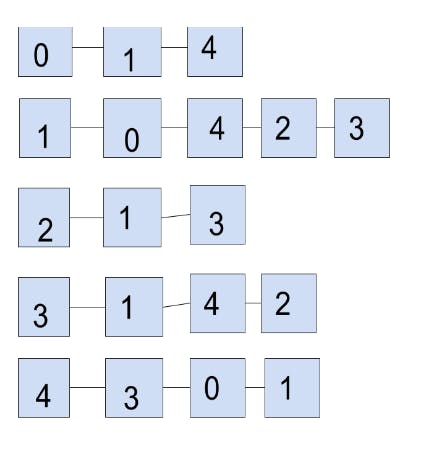
Implementation of adjacency list

class Node:
    """
    creating a node to connect
    to our main adjacency list
    """

    def __init__(self, data):
        self.vertex = data
        self.next = None


class Graph:
    """
    this class represents a graph as an adjacency list. The size of the array will be the no.
    of the vertices "V"
    """

    def __init__(self, vertices):
        self.V = vertices
        self.graph = [None] * self.V

    def addEdge(self, src, dest):
        # Adding the node to the source node
        node = Node(dest)
        node.next = self.graph[src]
        self.graph[src] = node

        # Adding the source node to the destination
        # as a undirected graph
        node = Node(src)
        node.next = self.graph[dest]
        self.graph[dest] = node

    # printing the graph
    def printGraph(self):
        for i in range(self.V):
            print("Adjacency list of vertex {}\n head".format(i), end="")
            temp = self.graph[i]
            while temp:
                print(" -> {}".format(temp.vertex), end="")
                temp = temp.next
            print


def main():
    graph = Graph(5)  # graph of 5 vertices
    graph.addEdge(0, 1)
    graph.addEdge(0, 4)
    graph.addEdge(1, 2)
    graph.addEdge(1, 3)
    graph.addEdge(1, 4)
    graph.addEdge(2, 3)
    graph.addEdge(3, 4)

    graph.printGraph()


if __name__ == "__main__":
    main()

Output : Adjacency list of vertex 0 head -> 4 -> 1 Adjacency list of vertex 1 head -> 4 -> 3 -> 2 -> 0 Adjacency list of vertex 2 head -> 3 -> 1 Adjacency list of vertex 3 head -> 4 -> 2 -> 1 Adjacency list of vertex 4 head -> 3 -> 1 -> 0